Final Project
Human to Robotic arm interface
First idea and inspiration
Most of this is mentioned in the week 1. So here I will talk about inspirations for the design of my part. While searching on the internet, I found this video:
DIY VR Haptic Gloves
And I decided to repurpose the design of finger sensors for a shoulder joint. The idea was to connect the base of the neck, pecks and back to the elbow using string and spools. Then to read those 3 distances and from them, using many constraints that the system has, calculate the angles of the shoulder.
At first I’ve designed a holder for those spools that would be place on the shoulder.
The ring was made to fit my own shoulder with diameter of 120 mm. Later, after printing it, turned out it didn’t make any sense to print the lower part of it, because you couldn’t lower your hand because of it. So I’ve cut it out.
 The shoulder ring with a cut in the lower portion, and spools already attached
The shoulder ring with a cut in the lower portion, and spools already attached
The next challenge was making the spools. First of all, the project that I took them from, used 300 degree potenciometers because it was enough for fingers. It wasn’t enough for a shoulder. At first the idea was to use 3000 degree potentiometers, but they didn’t have a cutout in the middle to stuff the spring of the spool in them. And with high price trying to make a cut ourselves really didn’t work out. So in the last moment we switched to using rotary encoders, they also didn’t have cutouts in the middle, but they were made from a much softer metal, and we made the cutouts ourselves.
 Rotary encoder with a self made cut
Rotary encoder with a self made cut
After printing the spool casings, assembling them, was the worst part of the project. Because we couldn’t make the cuts deep enough to hold the spring, it needed to be glued to the encoder. As you can imagine, gluing something this small and where all the parts need to spin after, was a nightmare. Also just finding office badge holders for all the parts needed was a challenge as only 1 out of 4 shops that I’ve checked, had them. In the end only 2 spools were working and up and down movements of the hand weren’t read well.
Spool casings being printed
 One spool already assembled and attached to the shoulder ring
One spool already assembled and attached to the shoulder ring
Here you can see the ring that was meant to attach the strings from those spools to the elbow, with the part that was meant to measure the elbow angle.
Elbow piece
And here’s a video of the whole thing in action, and printing data for elbow and wrist angles.
Before having the whole thing built, I started to work on the code to determine shoulder angles from measured distances. Not having much time, I’ve decided to use python, and matplotlib for visualization. The main part of the algorithm was to make a function that would move a triangle of elbow points around the sphere that was defined by the shoulder, and minimize any inconsistancies with the constraints of the system such as: distances between points of two triangles, length between elbow and a shoulder (radius of the sphere on which the triangle is moved), and the orientation of the triangle as the arm can be rolled only from 0 to 180 degrees.
Here’s the code for the main computation:
import numpy as np
from scipy.optimize import minimize
class Compute():
def __init__(self, S_points, distances, angle_degrees=90) -> None:
self.S_points = S_points
angle_radians = np.deg2rad(angle_degrees)
rotation_matrix = np.array([[np.cos(angle_radians), 0, np.sin(angle_radians)],
[0, 1, 0],
[-np.sin(angle_radians), 0, np.cos(angle_radians)]])
self.E_points = np.dot(S_points, rotation_matrix.T)
self.E_points[0, 1] += distances[0]
self.E_points[1, 1] += distances[1]
self.E_points[2, 1] += distances[2]
self.joint_center = np.mean([self.S_points[0], self.S_points[2]], axis=0)
print("Joint center:", self.joint_center)
self.joint_sphere_radius = np.mean([np.linalg.norm(self.E_points[0] - self.joint_center),
np.linalg.norm(self.E_points[0] - self.joint_center),
np.linalg.norm(self.E_points[0] - self.joint_center)])
print("Joint sphere radius:", self.joint_sphere_radius)
def find_elbow_points(self, real_E_points, distances, angle):
initial_triangle = [
np.linalg.norm(self.E_points[0] - self.E_points[1]),
np.linalg.norm(self.E_points[1] - self.E_points[2]),
np.linalg.norm(self.E_points[2] - self.E_points[0])
]
circle_params = []
for i in range(3):
S_radius = distances[i]
params = self.find_circle_intersection(self.S_points[i], S_radius, self.joint_center, self.joint_sphere_radius)
if params is None:
raise ValueError(f"No intersection found for sphere {i}")
circle_params.append(params)
E_points = self.place_points_on_circles(circle_params, initial_triangle)
# Calculate the center of the triangle (between E1 and E3)
E1, E2, E3 = real_E_points[0], real_E_points[1], real_E_points[2]
center_point = (E1 + E3) / 2
# Create a normal vector to the triangle at the center point
normal_vector = np.cross(E2 - E1, E3 - E1)
normal_vector /= np.linalg.norm(normal_vector) # Normalize the normal vector
# Define the distance for O_point calculation
distance = 1.0
# Calculate the first O_point along the normal vector
O_point1 = center_point + distance * normal_vector
# Calculate the second O_point based on the angle, rotating around the first O_point
angle_radians = np.deg2rad(angle)
rotation_matrix = np.array([
[np.cos(angle_radians), -np.sin(angle_radians), 0],
[np.sin(angle_radians), np.cos(angle_radians), 0],
[0, 0, 1]
])
offset = rotation_matrix @ (O_point1 - center_point)
O_point2 = O_point1 + offset
O_points = np.array([O_point1, O_point2])
return E_points, O_points
def objective(self, angles, circle_params, initial_distances):
E = self.circle_points(angles, circle_params)
E1, E2, E3 = E[:3], E[3:6], E[6:9]
d12 = np.linalg.norm(E1 - E2)
d23 = np.linalg.norm(E2 - E3)
d31 = np.linalg.norm(E3 - E1)
# Add penalties to break symmetry and enforce non-negative y-coordinates
penalty = max(0, E3[2] - E1[2]) + \
max(0, E1[0] - E2[0]) + \
1e3 * sum(max(0, -point[1]) for point in [E1, E2, E3])
# + max(0, E3[2])
return (np.abs(d12 - initial_distances[0]) +
np.abs(d23 - initial_distances[1]) +
np.abs(d31 - initial_distances[2]) + penalty)
def find_circle_intersection(self, S_center, S_radius, J_center, J_radius):
d = np.linalg.norm(S_center - J_center)
if d > S_radius + J_radius:
return None # No intersection
if d < abs(S_radius - J_radius):
return None # One sphere is within the other
if d == 0 and S_radius == J_radius:
return None # The spheres are coincident
a = (S_radius**2 - J_radius**2 + d**2) / (2 * d)
h = np.sqrt(S_radius**2 - a**2)
P2 = S_center + a * (J_center - S_center) / d
ex = (J_center - S_center) / d
# Determine basis vectors in the plane of intersection
ey = np.cross(ex, np.array([0, 0, 1]))
if np.linalg.norm(ey) < 1e-10: # Handle edge case where ey is nearly zero
ey = np.cross(ex, np.array([0, 1, 0]))
ey /= np.linalg.norm(ey)
ez = np.cross(ex, ey)
center = P2
radius = h
return center, radius, ex, ey, ez
def place_points_on_circles(self, circle_params, initial_distances):
initial_angles = [0, 2 * np.pi / 3, 4 * np.pi / 3]
result = minimize(lambda angles: self.objective(angles, circle_params, initial_distances),
initial_angles, method='L-BFGS-B')
optimized_points = self.circle_points(result.x, circle_params)
return optimized_points.reshape((3, 3))
def circle_points(self, angles, circle_params):
points = []
for i in range(3):
center, radius, ex, ey, ez = circle_params[i]
angle = angles[i]
point = center + radius * (np.cos(angle) * ez + np.sin(angle) * ey)
points.append(point)
return np.concatenate(points)
def get_circle_params(self, distances):
circle_params = []
for i in range(3):
S_radius = distances[i]
params = self.find_circle_intersection(self.S_points[i], S_radius, self.joint_center, self.joint_sphere_radius)
if params is not None:
circle_params.append(params)
return circle_params
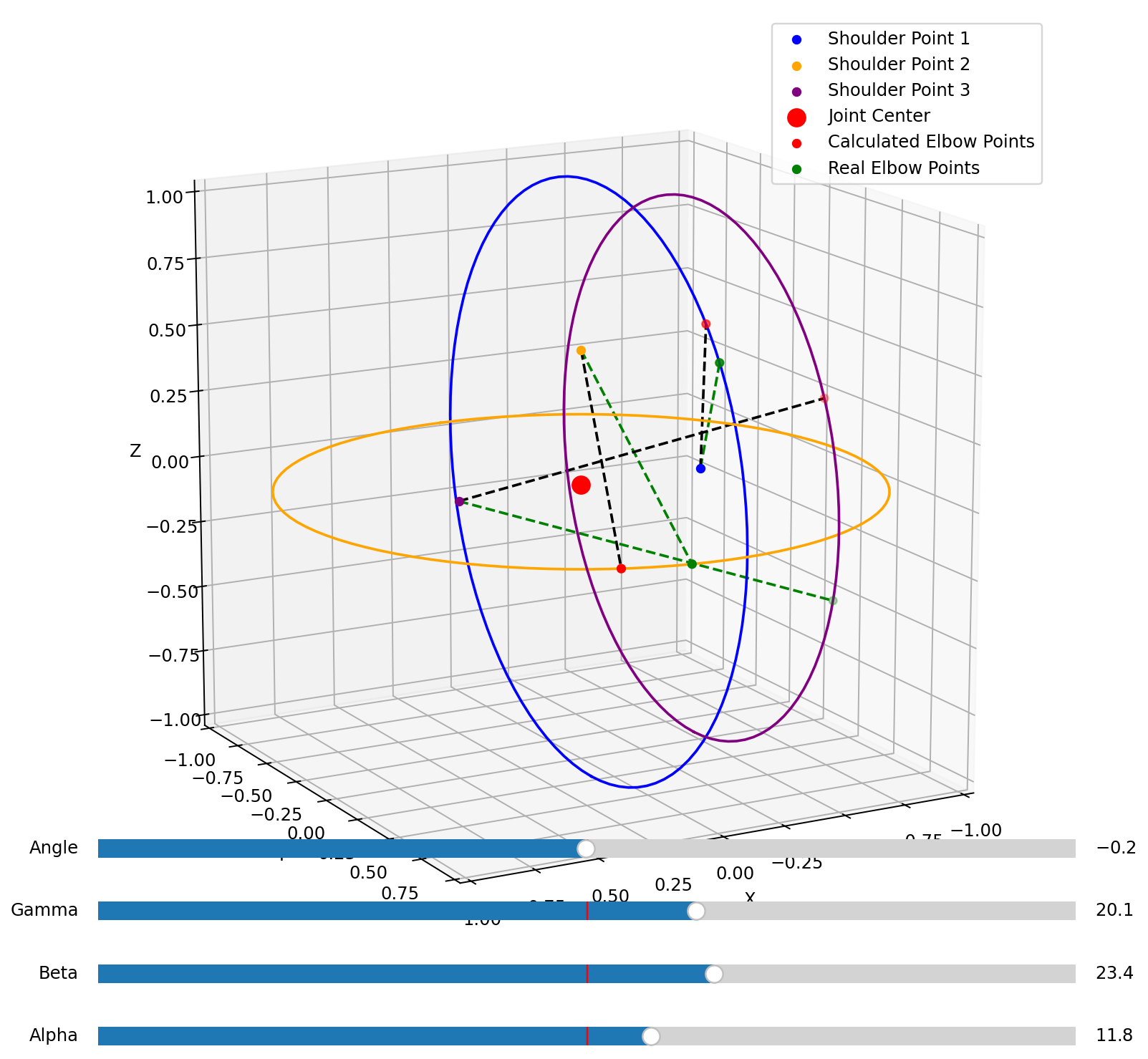 Example of computing the red points from given distances, with green points as reference
Example of computing the red points from given distances, with green points as reference
As you can see, the minimalization algorithm and the cost function could be much improved to increase the precisions and eliminiate any symmetries of the system.